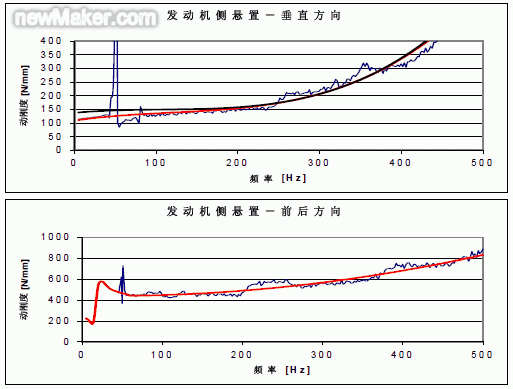
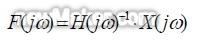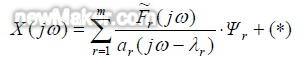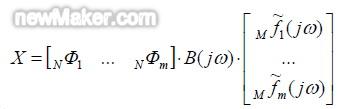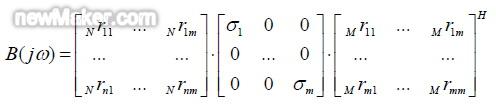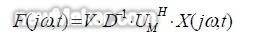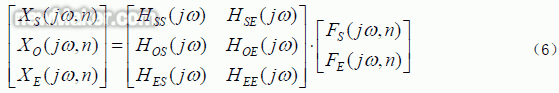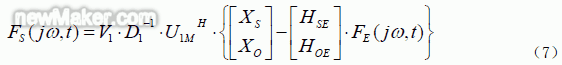|
摘 要:在关系到车辆NVH 性能的减振系统的仿真分析中,获取减振元件车体侧和/或振源侧接附点在实际车辆运行中的载荷力是十分关键的,作为模型输入的该载荷力的精确性将直接影响计算分析结果。在本文中介绍了以工作模式下车辆参考点响应信号和从响应点到接附点的传递函数来识别载荷力的方法以从相关的试验数据中得到所述的载荷力。 1 背景介绍 1.1 车辆减振元件的接附点载荷力 在进行车辆NVH 性能仿真分析中,获取减振元件的车体侧和/或振源侧接附点在确定实际车辆运行中的载荷力是十分关键的。如将车辆和/或车辆的子系统看作是振动系统,并在工作点附近作线性化假设,则所述的载荷力是系统的输入,它经过系统的传递达到车辆内部,引起相应的振动噪声响应。 另外,来自某一振源的结构振动作为能量传入车内,如果事先确定了分析截面,则经过该截面的各传递路径将对作为目标的车内振动和噪声产生不同的贡献量,如需进行贡献量分析,也需要得到位于分析截面上的减振件接附点上的载荷力,包括各载荷力的辐值和相对相位关系。 专业研发、生产、销售:测漏机,检漏机,试漏机,测漏仪,塑料瓶装袋机,垫片冲裁入盖机,客服热线:13929416960. 本文中典型地以动力总成(发动机+变速箱)造成的振动经过动力总成悬置和车辆的前悬架传入的例子进行本方法的阐述。在对测试数据的处理中,主要采用了奇异值分解方法(SVD)以及以它为基础的矩阵伪逆计算。 在本文中为方法介绍的目的使用了自行编写的程序进行简单的计算,但对于真实工作中遇到的大型问题则需要工程化软件来支持计算。近来比利时LMS 公司发布的Virtual.Lab 系列软件提供了强大的载荷力识别功能,可以基于实际测量中获得的大量数据自动的进行相关的载荷力识别,从而为其他相关的分析工作,例如强度分析、NVH 分析、耐久性分析等提供可靠的载荷条件。 1.2 车辆减振元件的接附点载荷力 在下节中将详述,本方法的核心工作是计算系统(MIMO 形式)的传递函数矩阵的伪逆。例如需要识别m 个力,则一般因为测试误差等因素测试点个数n 大于m,以保证测试的可靠性和精度。以奇异值分解方法计算矩阵伪逆的实质是在酉空间求不相容方程组的极小范数最小二乘解,理论阐述可详见文献[1],此处不赘述。 2 载荷力识别方法原理 专业研发、生产、销售:植草板,植草格,排水板,蓄排水板,卷材排水板,植草板厂家,客服热线:0755-23937035. 2.1 载荷力识别方法的模态空间解释 原则上如果需要识别m 个载荷力,只需测定m 个响应即可,即得到m×m 维度的传递函数矩阵并对其进行逆矩阵计算来确定载荷力,如式(1)所示,本节中在状态空间中描述,为简化仍采用m 和n 描述矩阵维度(即真实识别的载荷力的维度为m/2):
因此,使用SVD 方法得到载荷力的识别结果为:
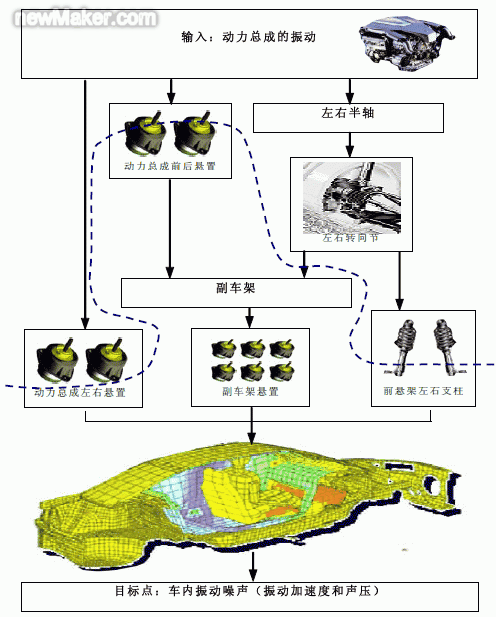
2.2 载荷力识别方法的原理步骤 原设在系统中为识别m 个力(m 个输入点)而布置了n 个加速度传感器(n 个参考点),并使得n>m,则分两步进行载荷力识别。 第一步:测定在典型的工况下车辆上n 个参考点处的加速度响应谱,这些响应是由待估计的m 个载荷力造成的; 第二步:将相关的振源去除而测定从m 个输入点到n 个参考点的n×m 维的传递函数矩阵H; 第三步:对所测得的传递函数矩阵进行SVD 计算,并按照式(1)计算出m 个载荷力谱的识别结果。 在第三步中如果典型工况为稳态工况,例如怠速工况,则可在每个频率点下进行,如果是非稳态工况,例如典型的2 档加速工况,则可在转速—频率空间中对应于发动机转速特征阶次,特别是2 阶和4阶的斜线带内进行,而估计出相应阶的分力谱。 注意:上述各步骤均为复数运算,且力均为力矢量,在实际计算中需要分别计算其三个分量。 3 载荷力识别方法在工程实践中的使用 3.1 工程实践中的使用步骤 在进行汽车NVH 设计,特别是与发动机悬置、车辆悬架等部件相关的设计与优化匹配中,确定此类部件输入给车体接附点的载荷力是关键的。无论是采取对振源减振的处理方法,还是进行对从振源到车内目标点传递路径的修改,准确的获得典型工况下或导致车辆发生NVH 问题的关键工况下的载荷力是必不可少的工作。 载荷力的选择可按如下步骤进行。 第一步,确定所研究的NVH 的振源。导致汽车乘员舱内噪声响应的典型振源例如但不限制于是动力总成的振动。因此,在本节的例子中选择动力总成作为振源进行载荷识别。 第二步,确定从所述的振源到被评价的目标点之间的声振传递路径。一方面,在实际车辆中随车体和底盘结构的差异,传递路径变化多样;另一方面,对于某一车辆,因为动力总成和车体之间存在多种传力渠道,因此传递路径也很繁杂。为此,应根据具体问题抓住矛盾的主要方面,忽略非主要影响因素来确定传递路径。例如在本节的例子中选择了四个从动力总成到乘员舱内目标点的声振传递路径,如在图1 中示出且在表1 中列出。 第三步,确定主动侧与被动侧的分界面。在确定此分界面时需要考虑到待分析问题的性质。例如,“串联”在传递路径内的某部件作为主动侧(振源侧)还是被动侧(响应侧)需要考虑到此部件在整个分析工作中的地位。借用电学量进行机电类比,可将振源(动力总成激振力)看作“复电流”I,而将车体与声腔耦合面处某点的结构振速看作“复电压”U,从振源到该点的传递路径的特征因而用复阻抗表示[4,5]。由于汽车结构的复杂性,该传递路径可能由多个子路径综合而成。由于分析工作的对象不同,可能其中有些近振源侧子路径的特征不在分析范围内,此时可将该子部分的阻抗看作电流源(振源的总力)的“内阻抗”从而将这部分对应的振速“压降”折算到电源内以将其从分析系统中隔离去。合理的隔离对于选择合适的试验点、简化复杂模型和有效地利用试验数据是十分重要的。隔离“内阻抗”后即完成了主动侧与被动侧的分界面的确定。在图1 中虚线示出了对本文中示例的界面划分。
3.2 载荷识别实例 现对某一欧洲B 级轿车的动力总成悬置接附点和左右前悬架支柱接附点处输入给车体的各载荷力进行计算,以估计由动力总成和前悬架传递给车体的载荷力。计算中所需的响应和传递函数由LMS 公司的测试软件Test.Lab 实测得到。此处涉及到的各待识别力为动力总成在II 档加速典型工况下的结果以利用该方法进行识别。
表1 以动力总成为振源的车内噪声传递路径汇总表
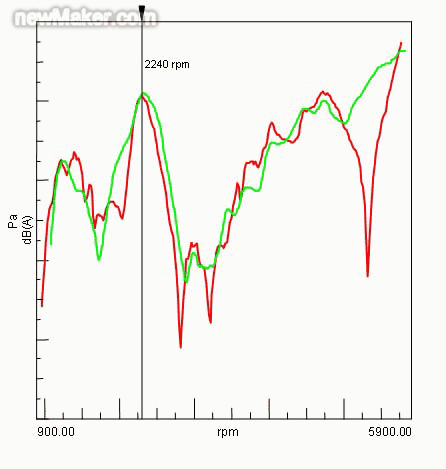
另外,在以上的SVD 原理推导中沿频率轴进行逐频率点识别,而此处的工程实例中在频率-转速平面内沿发动机二阶振动对应的带内进行识别,因为最大的载荷力将一般地出现在该带内。更特定地,在底盘测功机上进行的II 档加速试验中,发现在发动机2240rpm 处存在车内噪声声压的极值,因此对该二阶带与该转速线的交点处进行了识别。另外,还对怠速工况进行了二阶频率点上的载荷力识别。
在上述两个识别转速点上,分别给出了如下各接附点的载荷力识别结果作为示例,分别为左侧控制臂接附点CL、右侧控制臂接附点CR、前侧动力总成悬置接附点EF 和后侧动力总成悬置接附点ER,见图3 中所示。
(a)II 档加速2240rpm 下识别结果 CL(后部接附点):81.44 N(Y 方向);CR(后部接附点):83.05 N(Y 方向)。但是这两个力在该转速下的相位基本为反相的,考虑到车体大致的横向对称性,它们在整车内部的作用将很大程度上互相抵消,但是较大的载荷力幅值将引起局部较大的振动。 EF:13.49 N(Z 方向);ER:18.66 N(Z 方向)。这两个垂向载荷力主要提供车辆运行中动力总成的倾覆反力矩。它们也是动力总成总输出转矩中的二阶交流成分进入车体的主要渠道,因此这两个力的确定对于整车的NVH 分析十分重要。 (b)怠速工况识别结果 CL(后部接附点):5.86 N(Z 方向);CR(后部接附点):14.06 N(Z 方向);EF:10.80 N(Z 方向);ER:23.32 N(Z 方向)。可见,在怠速工况下,主要的载荷力出现在后悬置的Z 方向上,从此处向车体输入振动能量,导致与怠速相关的车辆NVH 问题。
本文中以振动工程中常用的SVD 方法处理传递函数矩阵以估计由车辆的悬置系统和悬架系统输入给车体的载荷力。此处使用的SVD 方法的实质是以n 维酉空间内的矢量来最佳逼近它的m 维子空间内的矢量,即在某频率点(或对非稳态信号在时频微元的中心点)上以最小二乘法求解带冗余方程的传递函数方程组的逆问题,从而得到各接附点的载荷力谱。该方法由于允许处理冗余信息,因此与传统的逆矩阵方法相比提高了识别算法的精度和稳定性。 本文进一步通过工程实例论述了如何将原理性步骤应用于工程实践中。为此给出了用于识别造成乘用车的振动噪声响应的振源所产生的载荷力的方法步骤,并针对悬置软垫这类典型元件给出了与动刚度法相结合的载荷力识别方法。 文中为从原理角度阐述问题起见使用了简化情况,但对于复杂的工程实际问题需要借助于合适的软件进行有效的分析。LMS 公司发布的Virtual.Lab 系列软件提供了强大的载荷力识别功能,可以基于实际测量中获得的大量数据自动的进行相关的载荷力识别,从而为NVH 分析工作提供有利的输入载荷数据。 参考文献 [1] 方保鎔.矩阵论.[M].北京:清华大学出版社, 2004. [2] 李德葆.试验模态分析及其应用. [M].北京:科学出版社, 2004. [3] 李方泽.工程振动测试与分析. [M].北京:高等教育出版社,1992. [4] 官飞.理论力学. [M].北京:清华大学出版社,1995. [5] Leo L. Beranek.Acoustics. [M]. Cambridge, MA: Acoustical Society of America,1993.(end) |